The Earth’s rotational rate is ever changing, due to a series of factors, mainly the effect of tidal friction caused by the Moon and the effect of the rebounding of the Earth’s crust since the disappearance of the ice accumulated during the last Ice Age. It would be then very impractical to base timekeeping on this ever changing rate. So, for practical purposes, we use UTC (Universal Coordinate Time), a compromise between TAI (International Atomic Time), the uniform time based on atomic clocks, and UT1 (Universal Time), the mean solar time based on the actual Earth’s rotation. UTC has been in existence before 1972 but it is in 1972 that the current mechanism of inserting leap seconds was implemented.
Atomic clocks tick at a uniform rate based on the International System of Units (SI) definition of second (i.e. 9192631770 oscillations of a certain hyperfine transition of Cesium-133). Being based on a physical phenomenon, and not on the Earth’s rotation, atomic clocks constitute a uniform standard. The time they measure is called TAI. When 86400 (=60 x 60 x 24) of these SI seconds elapse, a day elapses in TAI.
We are nevertheless usually accustomed to define time in relation to the Earth’s rotation. UT1 is a mean solar time and it is based on Earth’s rotational rate that influences the length of the mean solar day (LOD). As LOD is very close to 86400s (a day according to atomic time), we can plot the excess of LOD over an “atomic” day to see how it evolves through time. This excess amounts to just a handful of milliseconds, it evolves rather chaotically but it exhibits seasonal variations: LOD is slightly longer during Northern Hemisphere winters and slightly shorter during Northern Hemisphere summers.
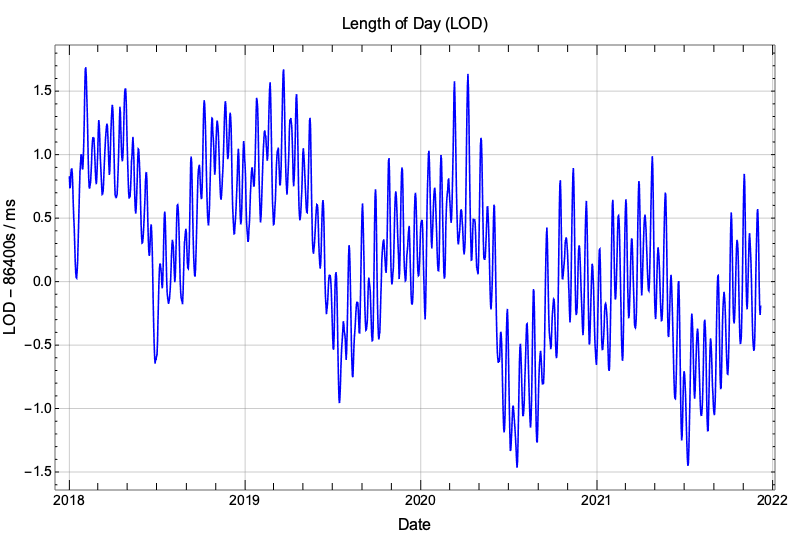
UT1 is based on this mean solar day and its variable ticking rate is due to the accumulated variations of LOD. To assess the impact of LOD on UT1, we should look at the trend of LOD through the years, for example by taking a moving average to smooth away all its high frequency variations. The following plot shows the evolution of LOD and of its trend since 1972, the year the leap second mechanism was introduced into UTC.
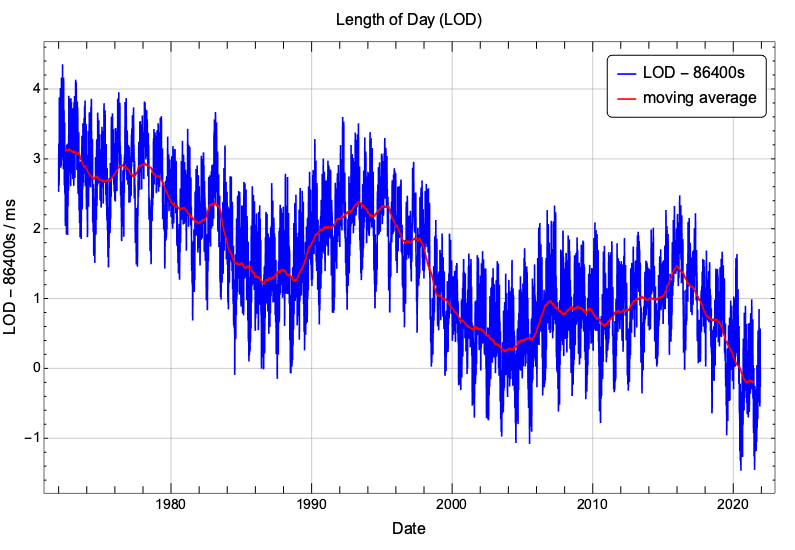
LOD was around 3ms slower (on average) than 86400s in the early seventies but it has been trending down and nowadays it is slightly faster (on average) than 86400s. At times LOD is shortening, meaning that the Earth’s rotational rate is overall accelerating, and at times it is lengthening, meaning that the Earth’s rotational rate is overall decelerating.
Since 1972, LOD has mainly been longer than 86400s causing UT1 to run slower than TAI, no matter if the Earth’s rotational rate was accelerating or decelerating. Because UT1 has been lagging behind TAI, we expect the difference (UT1 – TAI) to have been growing larger (in absolute value) and that is exactly what the next graph shows. We notice that the slope of the graph is not constant and this reflects the periods of acceleration and deceleration of the Earth’s rotation.
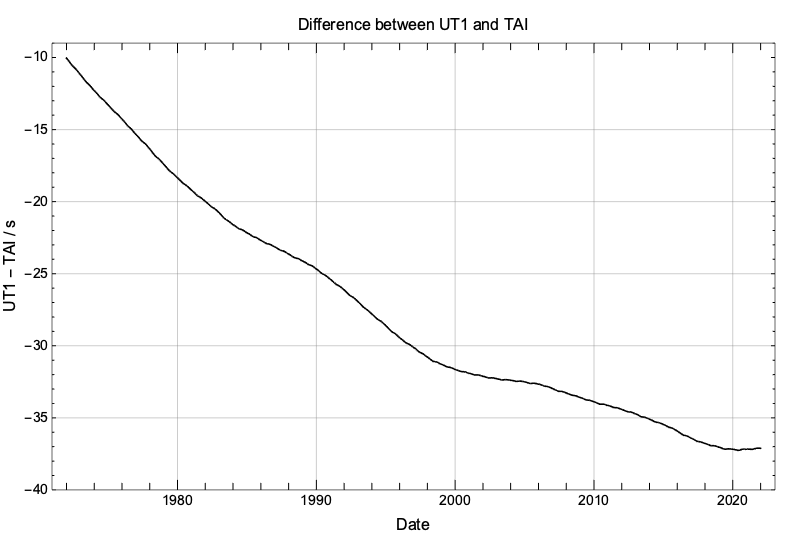
UTC, the universal coordinated time, is a discontinuous time scale that ticks at the same rate as TAI but that occasionally inserts “leap seconds” to approximately follow UT1. The following graph shows how the differences between UT1 and UTC from TAI have been evolving since 1972. The function (UTC – TAI) is piecewise constant, ensuring a uniform rate for UTC, but presents discontinuities every time a leap second is inserted.
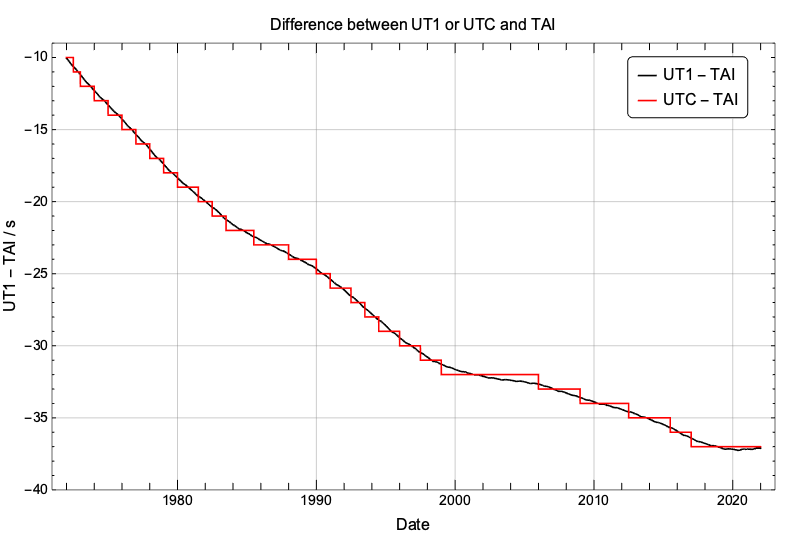
A leap second are inserted only at two specific times of the year: at the very end of June 30th or at the very end of December 31st (correction: Dave Herald has kindly pointed out that the standard allows for the insertion of leap seconds also at the end of March and at the end of September, but that has never occurred so far). The insertion happens by inserting a 60th second to the last minute of the day in the following manner: … 23h 59m 58s, 23h 59m 59s, 23h 59m 60s, 00h 00m 00s, 00h 00m 01s … Leap seconds were inserted more often in the seventies because LOD was, on average, 2-3ms slower than 86400s, so UT1 was ticking at a slower rate than today and lagging behind at a faster rate. Because LOD has been, on average, less than 1ms slower than 86400s since the early 2000’s, the need to insert leap seconds has consequently been less frequent.
The insertion of a leap second into UTC occurs every time the difference (UT1 – UTC) is forecast to get close or to become larger than -0.5s on June 30th or December 31st. The decision is taken by IERS, the International Earth Rotation Service in Paris and communicated around 6 months before it is planned to occur.
This graph shows how the difference (UT1 – UTC) has been kept within 1s since 1972. The discontinuity in this graph are due to the insertion of leap seconds into UTC. Because the decision to insert a leap second is taken around 6 months in advance and it is based on predictions, we can see a range of values for the observed difference (UT1 – UTC) at the time the leap second was inserted.
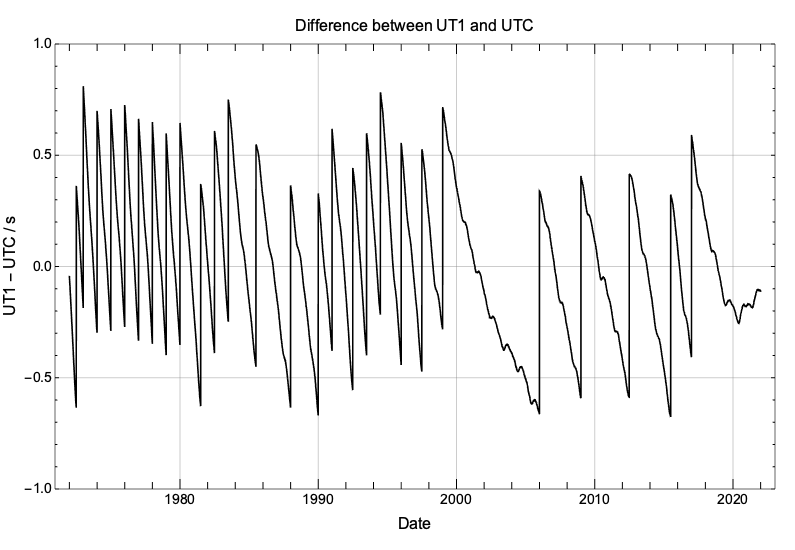
We are interested in understanding the possible scenarios for the insertion of a leap second before the 2023 annular-total eclipse, happening on April 20th. We would like to highlight that eclipse predictions are quoted in UTC, so predictions made one or more years in advance need to include a guess about a possible insertion of a leap second. If the predictions assume the insertion of a leap second but the leap second does not happen, all contact times will be off by 1s. The message is of course to use eclipse predictions that have been updated just before the eclipse, to ensure that all leap seconds have been accounted for and, equally important, that he prediction of the difference (UT1 – UTC) on eclipse day is reliable.
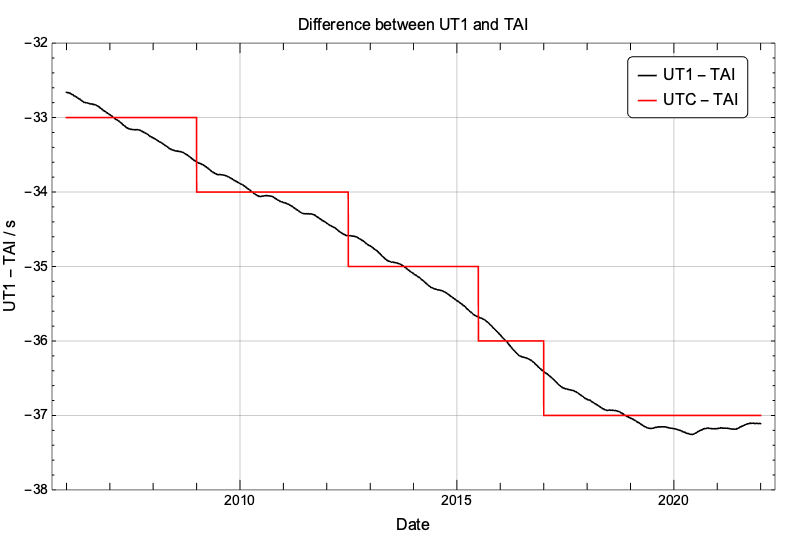
Let’s have a look at the recent behaviour of the difference (UT1 – TAI) and (UTC – TAI). Since the mid-2020, (UT1 – TAI) has been slightly increasing, a stark change for its almost steady decrease since 1972. The reason is to be found in the fact that the average value of LOD has become slightly smaller than 86400s in the very recent past, so UT1 is actually ticking slightly faster than TAI!!! The Earth’s rotational rate has been in a phase of steady acceleration since 2016. This is not that unusual: from around 1996 to around 2004, there has also been a long period of steady acceleration (causing LOD to decrease). But this time LOD has become slightly shorter than 86400s so we can actually see this trend reversal in the difference (UT1 – TAI). u
To guess what the future has in store, we can look at the predictions for 2022 of the difference (UT1 – UTC). The prediction is for the trend reversal to continue, that is to say for LOD to remain smaller than 86400s, sustained by a continuing trend of acceleration of the Earth’s rotational rate.
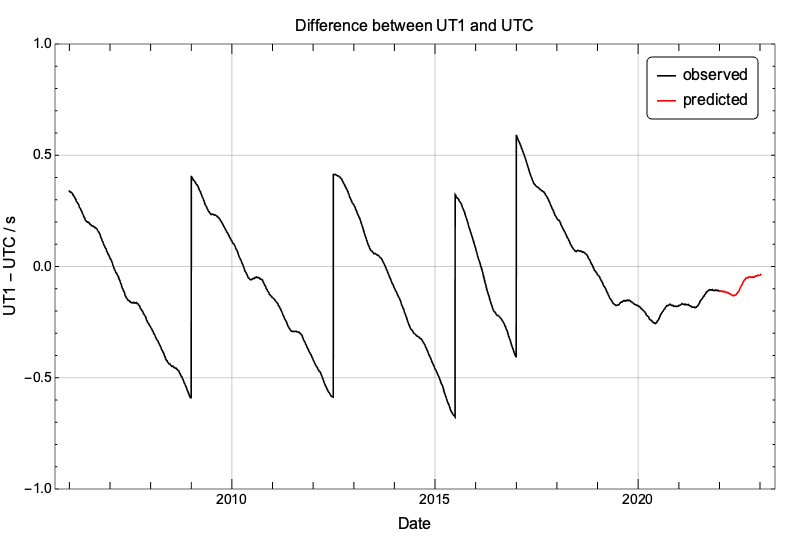
What are the implication of this trend reversal for the insertion of a leap second? It has been recently announced (https://datacenter.iers.org/data/latestVersion/bulletinC.txt) that there will not be any leap second added at the end of June 2022. And if we trust the predictions, it also seems very unlikely that there will be any leap second insertion at the end of December 2022. If that is the case, the difference UTC – TAI will stay at -37s, as it has been since the start of 2017, for the 2023 annular-total eclipse which is occurring in April.
Due to the stochasticity of the Earth’s rotational rate, forecasts worsen when the time horizon is longer than 6 months or so. There could still be a chance for the insertion of a leap second at the end of 2022 but it would require quite a trend reversal and a fast deceleration of the Earth’s rotation for the difference (UT1 – UTC) to reach a value around -0.5s by the end of 2022.
The Earth’s rotational rate has been accelerating since 2016, shortening LOD. During 1996-2004, we had an even longer period of acceleration, so it would not be unheard of for the acceleration to continue for another few years. In that scenario, the difference (UT1 – UTC) might grow even further and approach +0.5s. In that case, the insertion of a negative leap second would need to occur. Meaning that, more that inserting a second, a second will need to be removed from UTC. I guess this might happen in the following manner: … 23h 59m 57s, 23h 59m 58s, 00h 00m 00s, 00h 00m 01s … The second 23h 59m 59s would simply be skipped. The insertion of a negative leap second has never occurred since the introduction of leap seconds into UTC in 1972 due to LOD being longer than 86400s (and, as a consequence, UT1 ticking slower than TAI) but, now that LOD is slightly shorter than 86400s and UT1 is ticking faster than TAI, it would not be impossible for that to happen.
